W przypadku elementów ściskanych, traktowanych jako elementy wydzielone z bardziej złożonych ustrojów, uwzględnia się efekty II rzędu, jeśli smukłość tych elementów jest większa od wartości granicznej:
\[λ_c = \frac {l_0}{i} > λ_{lim}
\]
gdzie:
- l0 – długość efektywna elementu ściskanego zgodnie z poniższym rysunkiem:
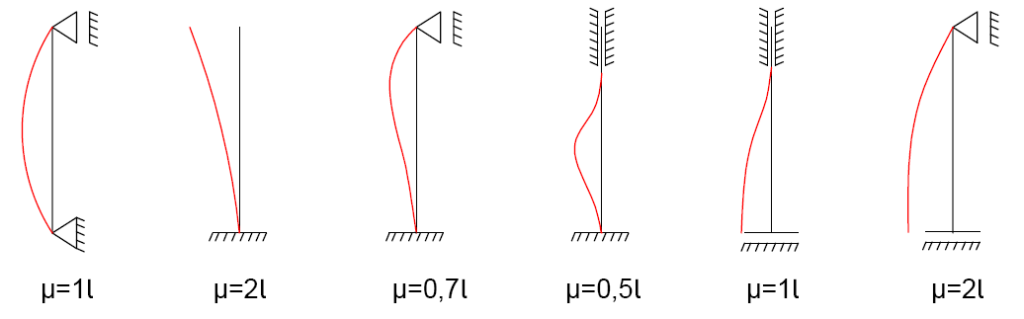
- i – promień bezwładności analizowanego niezarysowanego przekroju:
i = \sqrt{ \frac{J}{A_c}}
\]
Graniczna smukłość elementu λlim
Wyznaczenie granicznej smukłości elementu:
\[λ_{lim} = \frac { 20 \cdot A \cdot B \cdot C}{\sqrt{n}}
\]
gdzie:
- A – parametr zależny od współczynnika pełzania φef. W sytuacji, gdy wartość φef nie jest znana, to wartość współczynnika można przyjąć A = 0,7. W przeciwnym razie:
A = \frac {1}{1+ 0,2 φ_{ef}}
\]
- B – parametr uzależniony od pola przekroju całego zbrojenia w elemencie. Jeśli pole zbrojenia w danym elemencie nie jest znane, to można przyjąć, że B = 1,1. W przeciwnym razie:
B = \sqrt { 1+2 \cdot \frac {A_s \cdot f_{yd}} {A_c \cdot f_{cd}}}
\]
- C – parametr zależny od ilorazu momentów I rzędu na końcach elementu przy założeniu, że |M02| > |M01|. Jeśli wartości momentów nie są znane, to wartość współczynnika można przyjąć jako:
- C = 0,7, przy prostokątnym wykresie momentów,
- C =1,7, gdy wykres momentów jest trójkątny,
- W pozostałych przypadkach, np. gdy wykres jest antysymetryczny, można przyjmować współczynnik C = 2,7. W przeciwnym razie, przy znajomości wartości momentów, współczynnik C należy wyznaczyć według poniższego wzoru:
C = 1,7 – \frac {M_{01}}{M_{02}}
\]
- n – względna siła ściskająca w elemencie:
n = \frac {N_{Ed}}{A_c \cdot f_{cd}}
\]
Literatura:
[1] PN-EN 1992-1+AC+Ap 1,2,3 :2008, Projektowanie konstrukcji z betonu, Część 1-1: Reguły ogólne i reguły dla budynków,
[2] Zeszyt Edukacyjny Buildera Projektowanie Konstrukcji Zelbetowych WG EC2.
Zobacz też:
Wyboczenie sprężyste i niesprężyste