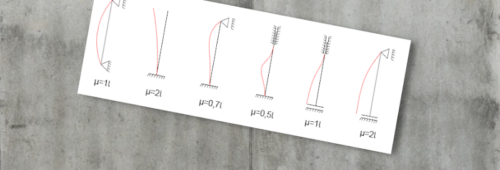
Metoda nominalnej sztywności pozwala na analizę elementów żelbetowych znajdujących się w układach statycznie niewyznaczalnych. Sztywność nominalną przekrojów żelbetowych określa się jako sumę sztywności (współczynników) betonu i zbrojenia, a także udziału zbrojenia.
\[EI=K_c \cdot E_{cd} \cdot I_c + K_s \cdot E_s \cdot I_s
\]
gdzie:
- KC – współczynnik zależny od wpływów zarysowania, pełzania,
- Ecd – obliczeniowa wartość modułu sprężystości betonu:
E_{cd}= \frac {E_{cm}}{1,2}
\]
- IC – moment bezwładności przekroju betonu,
- KS – współczynnik zależny od udziału zbrojenia:
- gdy stopień zbrojenia ρ ≥ 2‰, to można przyjąć współczynnik Ks=1,
- ES – obliczeniowa wartość modułu sprężystości zbrojenia,
- IS – moment bezwładności pola przekroju zbrojenia względem środka ciężkości powierzchni betonu.
Wyznaczenie współczynnika Kc:
\[K_c=\frac {k_1 \cdot k_2} {1+\varphi_{ef}}
\]
gdzie:
\[k_1=\sqrt{\frac{f_{ck}}{20}}
\] \[
k_2=\min{ \left[ \frac{n \cdot \lambda}{170} ; \quad 0,20\right ]}
\]
- n – względna siła osiowa wynosząca:
n=\frac {N_{Ed}} {N_{Rc} =A_c \cdot f_{ck} }
\]
- λ – smukłość elementu:
\lambda=\frac {l_0=L_{cr}}{i}
\]
- i – promień bezwładności przekroju niezarysowanego,
- φeff – efektywny współczynnik pełzania określany według poniższej zależności:
\varphi_{eff}= \varphi_0 \cdot k_{qp}
\]
Współczynnik powiększenia momentu
Oszacowanie całkowitego momentu obliczeniowego umożliwia zwiększenie momentu zginającego w stanie 2 rzędu za pomocą współczynnika amplifikacji według następującego wzoru:
\[M_{Ed}=M_{Ed,0} \cdot (1+a_B)
\]
w którym:
\[a_B= \frac{\beta}{\frac{N_B}{N_{Ed}}-1}
\]
gdzie:
- MEd,0 – moment pierwszego rzędu,
- β – współczynnik zależny od rozkładu momentów pierwszego i drugiego rzędu:
\beta=\frac{ \pi^2}{c_0}
\]
- c0 – współczynnik rozkładu momentu zginającego:
- w przypadku, gdy moment 1 rzędu jest stały wzdłuż elementu, to współczynnik c0 = 8,0,
- gdy rozkład momentu jest paraboliczny, to współczynnik c0 = 9,6,
- w przypadku trójkątnego rozkładu momentu współczynnik c0 = 12,0,
- jeśli moment jest liniowo zmienny, przyjmuje się moment zastępczy wynoszący:
M_0= ( 0,6 \cdot M_{02}- 0,4 \cdot M_{01} \ge 0,4 M_{02}) \quad i \quad c_0=8
\]
- NEd – obliczeniowa wartością siły podłużnej,
- NB – siła krytyczna ze względu na wyboczenie, obliczoną przy założeniu, że sztywność jest równa nominalnej.
Literatura:
[1] PN-EN 1992-1+AC+Ap 1,2,3 :2008, Projektowanie konstrukcji z betonu, Część 1-1: Reguły ogólne i reguły dla budynków,
[2] Zeszyt Edukacyjny Buildera Projektowanie Konstrukcji Żelbetowych WG EC2.
Zobacz też:
Efekty II rzędu przy ściskaniu