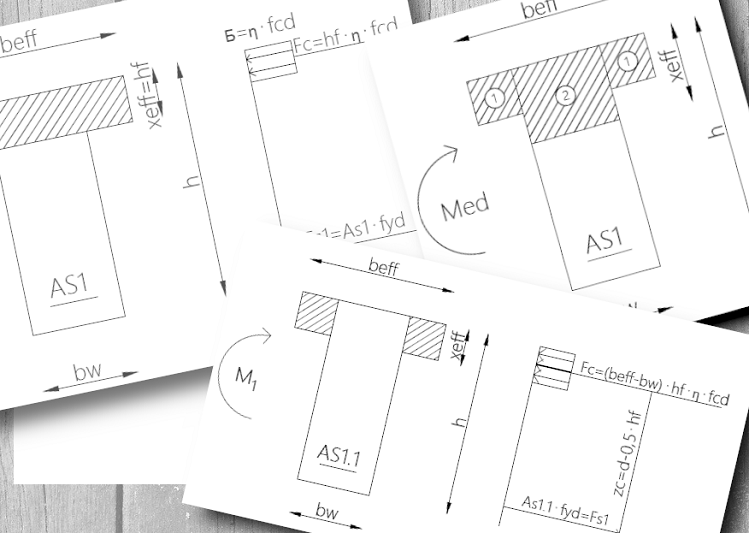
Podczas obliczeń zbrojenia przekroju teowego kluczową rolę odgrywa zasięg strefy ściskanej. W zależności od jej zasięgu rozróżnia się dwa następujące przypadki: przekrój pozornie teowy, gdy zasięg strefy ściskanej jest mniejszy od grubości półki oraz rzeczywiście teowy, gdy zasięg strefy ściskanej obejmuje całą półkę oraz część środnika. W związku z tym pierwszą czynnością, jaką należy określić przed przystąpieniem do obliczeń jest wyznaczenie zasięgu strefy ściskanej.
Względny zasięg strefy, w której beton ulega skróceniu ξeff
Wyznaczając względny zasięg strefy ściskanej możemy sprawdzić czy analizowany przekrój jest zbrojony podwójnie, czy pojedynczo. Sprawdzenie rozpoczynamy od wyznaczenia współczynnika μeff :
\(\mu_{eff} = \frac{M_{Ed}}{b_w \cdot d^2 \cdot \eta \cdot f_{cd}}
\)
gdzie:
- fcd – obliczeniowa wytrzymałość betonu na ściskanie,
- d – wysokość użyteczna przekroju: d = h – 0,1⋅h,
- η = 1,0, w przypadku, gdy: fck ≤ 50 MPa,
- η = (fck – 50)/200, w przypadku, gdy: fck > 50 MPa.
\xi_{eff} = \eta – \sqrt{\eta^2 – 2 \cdot \mu_{eff}}
\)
Wyznaczenie granicznej wartości ξeff,lim
\(\xi_{eff,lim} = \frac{\lambda \cdot \epsilon_{cu2}}{\epsilon_{cu2} + \epsilon_{yd}}
\)
gdzie:
- εcu2 – graniczne odkształcenie betonu,
- εyd – najmniejsze odkształcenie, podczas którego stal osiąga obliczeniową granicę plastyczności (εyd = fyd/Es),
- fyd – wartość obliczeniowa granicy plastyczności stali,
- Es – moduł sprężystości stali,
- λ – stosunek zasięgu strefy naprężeń ściskających do strefy skróceń:
- λ = 0,8, jeżeli: fck ≤ 50 MPa,
- oraz λ = 0,8 – (fck – 50)/400, jeżeli: fck > 50 MPa.
Przekrój jest pojedynczo zbrojony w przypadku, gdy ξeff ≤ ξeff,lim. Dalej skupimy się na wymiarowaniu przekroju teowego pojedynczo zbrojonego. Przekrój podwójnie zbrojony zostanie przeanalizowany w odrębnym artykule.
Przekrój teowy – określenie zasięgu strefy ściskanej
Wymiarowanie przekrojów teowych należy rozpocząć od określenia zasięgu strefy ściskanej. Najprostszą metodą sprawdzenia przekroju jest porównanie momentu MEd z tzw. momentem płytowym Mp. Zatem:
- gdy MEd ≥ Mp, to przekrój jest pozornie teowy,
- gdy MEd < Mp, to przekrój jest rzeczywiście teowy,
Moment płytowy to moment graniczny, w którym zasięg strefy ściskanej odpowiada grubości półki: xeff = hf :
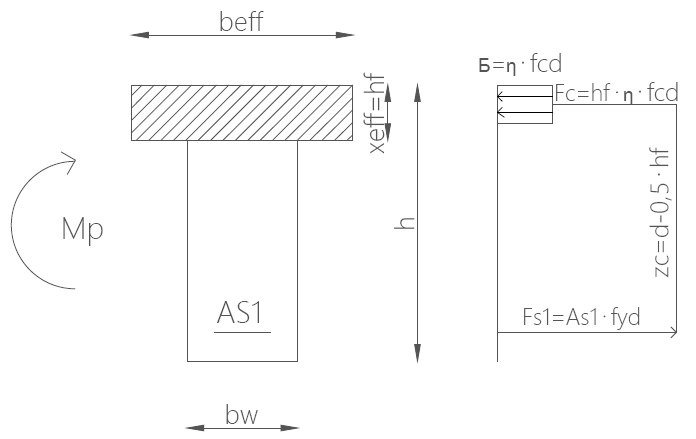
M_p = b_{eff} \cdot f_{cd} \cdot x_{eff} \cdot \left( d – 0,5 \cdot x_{eff} \right)
\)
Wymiarowanie zbrojenia przekroju pozornie teowego:
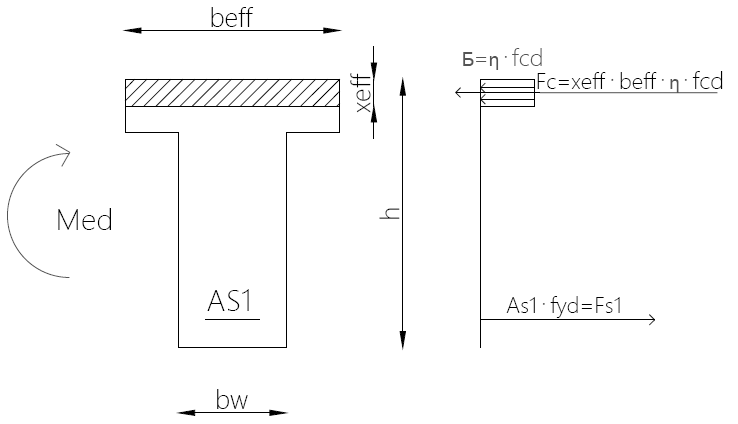
- Wyznaczenie zasięgu strefy ściskanej:
x_{eff} = \xi_{eff} \cdot d
\)
- Wyznaczenie pola przekroju zbrojenia:
A_{s1} = \frac{x_{eff} \cdot b_{eff} \cdot \eta \cdot f_{cd}}{f_{yd}}
\)
Wymiarowanie zbrojenia przekroju rzeczywiście teowego:
W przypadku przekroju rzeczywiście teowego należy rozpatrzeć dwa schematy oznaczone na poniższym rysunku:
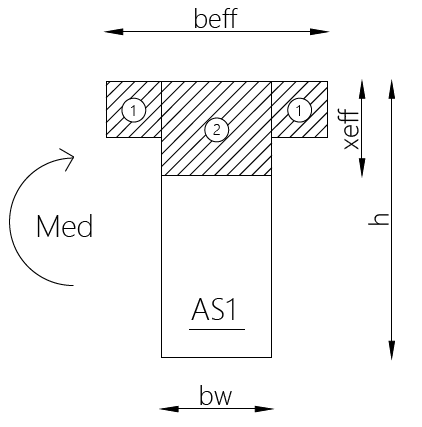
Schemat 1:
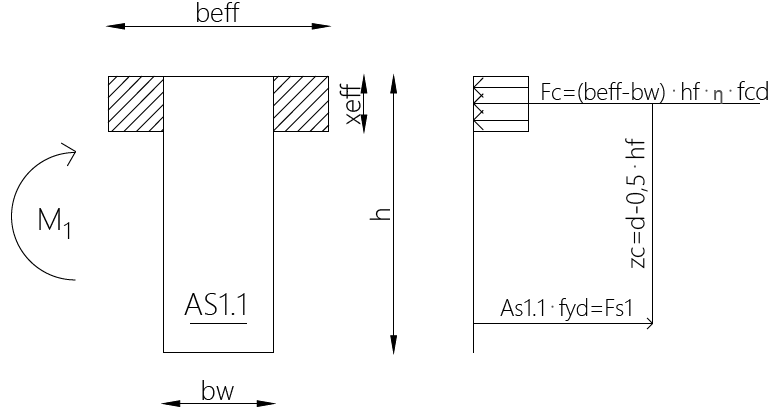
- Wyznaczenie momentu zginającego M1:
M_1 = h_f \cdot \left( b_{eff} – b_w \right) \cdot \left( d – 0,5 \cdot h_f \right) \cdot \eta \cdot f_{cd}
\)
- Wyznaczenie pola przekroju zbrojenia As1.1:
A_{S1.1} = \frac{M_1}{\left( d – 0,5 \cdot h_f \right) \cdot f_{yd}}
\)
Schemat 2:
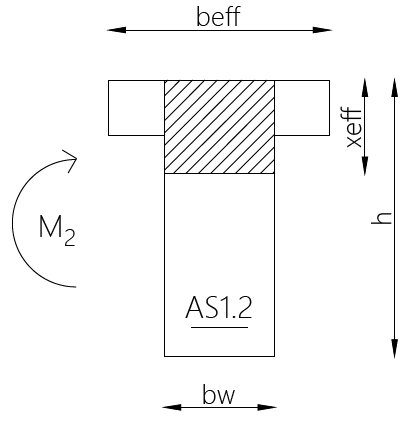
- Wyznaczenie momentu zginającego M2:
M_2 = M_{Ed} – M_1
\)
- Wyznaczenie współczynnika μeff:
\mu_{eff} = \frac{M_{2}}{b_w \cdot d^2 \cdot \eta \cdot f_{cd}}
\)
- Względny zasięg strefy ściskanej ξeff:
\xi_{eff} = \eta – \sqrt{\eta^2 – 2 \cdot \mu_{eff}}
\)
- Wyznaczenie zasięgu strefy ściskanej:
x_{eff} = \xi_{eff} \cdot d
\)
- Wyznaczenie pola przekroju zbrojenia As1.2:
A_{S1.2} = \frac{x_{eff} \cdot b_w \cdot \eta \cdot f_{cd}}{f_{yd}}
\)
- Ostatecznie pole zbrojenia przekroju:
A_{S1} = A_{S1.1} + A_{S1.2}
\)
Literatura:
[1] PN-EN 1992-1-1:2008 Eurokod 2 – Projektowanie konstrukcji z betonu – Część 1-1: Reguły ogólne i reguły dla budynków,
[2] PN-B-03264:2002 Konstrukcje betonowe, żelbetowe i sprężone – Obliczenia statyczne i projektowanie.
[3] Knauff, “Obliczanie konstrukcji żelbetowych według Eurokodu 2” Wydawnictwo Naukowe PWN, Warszawa 2012.
Zobacz też:
Odchyłki otulenia prętów zbrojeniowych