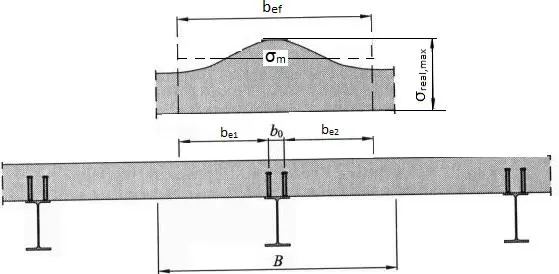
Szerokość współpracująca płyty żelbetowej konstrukcji zespolonych wprowadza się w celu uproszczenia obliczeń. Dzięki temu można przyjąć, że naprężenia ściskające σc w płycie są niezmienne na długości bef co przedstawia poniższy warunek:
\[N_c=b_{ef} \cdot \sigma_c = B\cdot \sigma_{real}
\]
w którym B stanowi szerokość płyty.
Szerokość współpracującą bef żelbetowej płyty podczas obliczeń można wyznaczyć z następującego wzoru:
\[\begin{equation} b_{ef} = b_0 +\sum \limits_i \beta_i \cdot b_{ei} \label{8} \end{equation}
\]
gdzie:
- b0 – odległość między środkami skrajnych ścinanych łączników po szerokości pasa,
- βi – współczynnik wynoszący odpowiednio:
- w przypadku podpory pośredniej βi = 1,0,
- dla podpory skrajnej βi=(0,55+0,025⋅Le/bei)≤1,0
- bei– efektywna szerokość betonowej półki liczona z każdej strony środnika. Można przyjąć bei=Li/8, lecz nie więcej niż wynosi geometryczna szerokość bi.
Wartość szerokości efektywnej można przyjąć jako odległość od skrajnego ścinanego łącznika do punktu w połowie odległości pomiędzy środnikami sąsiednich belek mierzoną w połowie grubości betonowej półki, poza przypadkiem, w którym odległość bi stanowi odległość od swobodnej krawędzi płyty.
Długość Le jest odległością między punktami zerowych momentów zginających. W przypadku typowych ciągłych zespolonych belek, w których obwiednia momentów pod różnymi układami obciążeń decyduje o Le oraz dla wsporników, Le może być określona w taki sposób jak przedstawiono na rysunku 2.
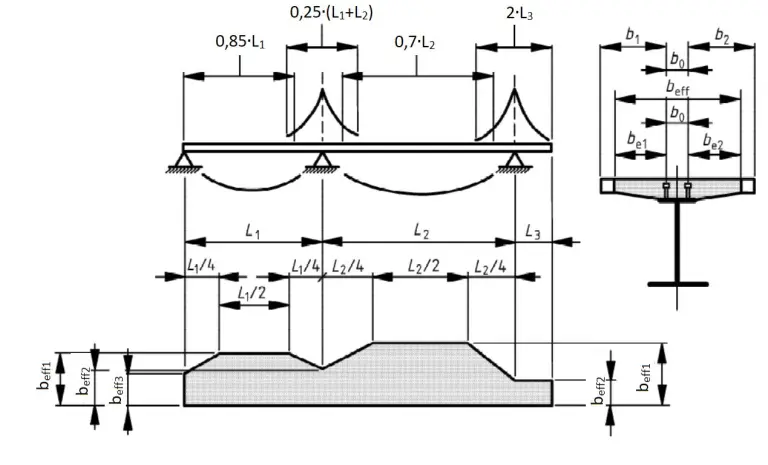
Rozpiętości Le z rys.2 odnosi się do konstrukcji z węzłami sztywnymi.
W przypadku ram lub belek z węzłami podatnymi (bądź przegubami Gerbera) długości te należy określić na podstawie wykresu rzeczywistych momentów zginających jako odległości między punktami zerowania się momentów.
W przypadku belek swobodnie podpartych o długości L i rozstawu belek s≥L/4 szerokość współpracującą bef wyznacza się według wzoru:
\[\begin{equation} b_{ef} = b_0 + L/8 + L/8 \approx L/4 \label{9} \end{equation}
\]
Literatura:
[1] PN-EN 1994-1-1 Projektowanie zespolonych konstrukcji stalowo-betonowych – Część 1-1: Reguły ogólne i reguły dla budynków.
[2] A.Biegus “Projektowanie zespolonych konstrukcji stalowo-betonowych według Eurokodu 4“.
[3] Access Steel, Lemaire, A. (2005, August). Arkusz obliczeniowy. Przykład obliczeń zespolonej belki drugorzędnej. Ptzykład SX014a-EN-EU,
[4] Szmigiera, E., Grzeszykowski, B., & Niedośpiał, M. (2019). Projektowanie konstrukcji zespolonych stalowo-betonowych. Część 1 Elementy zginane. Wydawnictwo Nau-kowe PWN.