Podczas obliczeń elementów ściskanych osiowo należy wyznaczyć współczynnik wyboczeniowy ꭓ zależny od smukłości względnej, parametru imperfekcji a także od odpowiedniej krzywej wyboczenia opisaną następującą funkcją:
\[\begin {equation} \chi= \frac{1}{\phi+\sqrt{\phi^2 -\overline \lambda^2}} \, \quad lecz \quad \chi \le 1,0 \label {9} \end {equation}
\]
gdzie:
\[\begin {equation} \phi=0,5\left [ 1+\alpha \cdot (\overline \lambda-0,2)+\overline \lambda^2\right] \label {10} \end {equation}
\]
W którym smukłość względną przy wyboczeniu giętnym należy wyznaczyć w zależności od klasy przekroju:
- w przypadku przekroju klasy 1, 2 i 3 smukłość względna wynosi:
\begin {equation} \overline \lambda =\sqrt{\cfrac{A_k f_y}{N_{cr}}} \label {8} \end {equation} = \frac {L_{cr}}{i} \cdot \frac {1}{\lambda_1}
\]
- w przypadku przekroju klasy 4 smukłość względna wynosi:
\overline \lambda =\sqrt{\cfrac{A_k f_y}{N_{cr}}} = \frac {L_{cr}}{i} \cdot \frac{\sqrt{\frac{A_{eff}}{A}}}{\lambda_1}
\]
gdzie:
- Ncr – siła krytyczna odpowiadająca miarodajnej postaci wyboczenia sprężystego, wyznaczona na podstawie cech przekroju brutto,
- Lcr – długość wyboczeniowa w rozpatrywanej płaszczyźnie wyboczenia,
- i – promień bezwładności przekroju brutto względem odpowiedniej osi,
- λ – smukłość graniczna przy osiągnięciu przez siłę krytyczną charakterystycznej wartości nośności przekroju, którą oblicza się ze wzoru:
\lambda_1=\pi \sqrt{\frac{E}{f_y}}=93,9 \varepsilon
\]
w którym współczynnik gatunku stali wynosi:
\[\varepsilon =\sqrt{\frac{235}{f_y}}
\]
Parametr Klasy imperfekcji α
Parametr Klasy imperfekcji α określa się w zależności od klasy imperfekcji ( rodzaju krzywej wyboczeniowej), przypisanej do kształtu przekroju, zgodnie z poniższymi tablicami:
Tabela 1. Parametry imperfekcji α krzywych wyboczeniowych [1]:

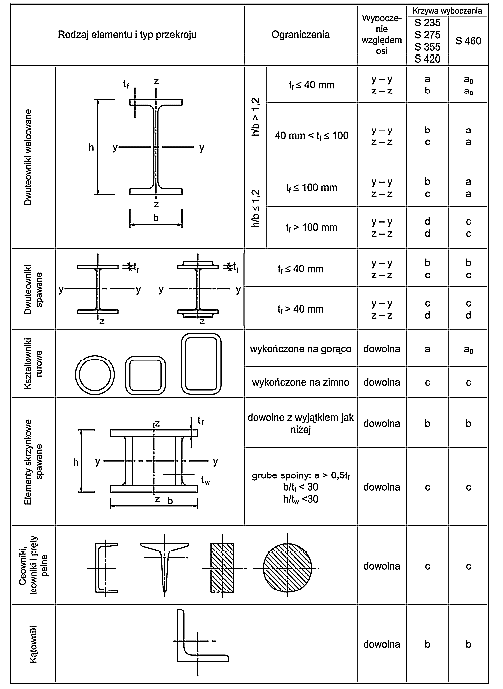
Tabela 2. Przyporządkowanie krzywych wyboczenia do rodzaju przekroju stalowego [1]:

Literatura:
[1] PN-EN 1993-1-1 Eurokod 3: Projektowanie konstrukcji stalowych – Część 1-1: Reguły ogólne i reguły dla budynków.
[2] A.Biegus “Projektowanie konstrukcji stalowych według Eurokodu 3.
Zobacz też:
Imperfekcje globalne i lokalne








