Ramy są konstrukcjami składającymi się z prętów w jednej płaszczyźnie. Pręty łączy się węzłami sztywnymi lub przegubami. Rama składa się ze słupów (pręty pionowe lub pochyłe) oraz rygli, czyli prętów poziomych. Ze względu na ich budowę można wyróżnić dwa rodzaje ram: o konturze otwartym oraz zamkniętym z dodatkowymi rozporami.
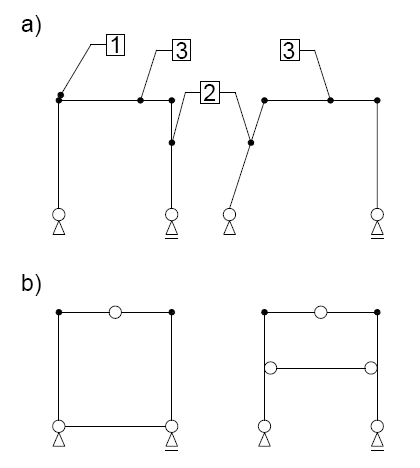
Ramy można również klasyfikować ze względu na:
- liczbę przęseł (jednoprzęsłowe lub wieloprzęsłowe),
- liczbę pięter (jednopiętrowe lub wielopiętrowe),
- kształt ramy (trójkątne, prostokątne, trapezowe, itp.).
Ze względu na sposób wyznaczalności wyróżnia się ramy statycznie wyznaczalne (izostatyczne) oraz statycznie niewyznaczalne (hiperstatyczne). Ramę oblicza się według następującego schematu:
- ustalenie schematu statycznego,
- wyznaczenie sił przekrojowych (wewnętrznych),
- sporządzenie wykresów.
W przypadku ram o konturze otwartym, siły przekrojowe oraz momenty zginające oblicza się wykorzystując równania równowagi, w innym wypadku stosuje się metodę przebiegów funkcyjnych (jest to tak zwana metoda przekrojów, w których redukowane są obciążenia do początku przedziału).
Warunek statycznej wyznaczalności ramy
Warunek statycznej wyznaczalności jest to tzw. warunek ilościowy. Sprawdzenie tego warunku mówi nam o tym czy analizowany układ prętowy będziemy mogli rozwiązać, czyli w praktyce wyznaczyć reakcje oraz siły przekrojowe. Jeśli ilość więzi w układzie jest zbyt mała, to układ nie jest nieruchomy, jeżeli więzi jest za dużo, w takim przypadku układ jest „przesztywniony”. W celu sprawdzenia warunku statycznej wyznaczalności należy spełnić poniższy warunek:
\[e = 3t
\]
gdzie:
e – liczba więzi,
t – liczba tarcz.
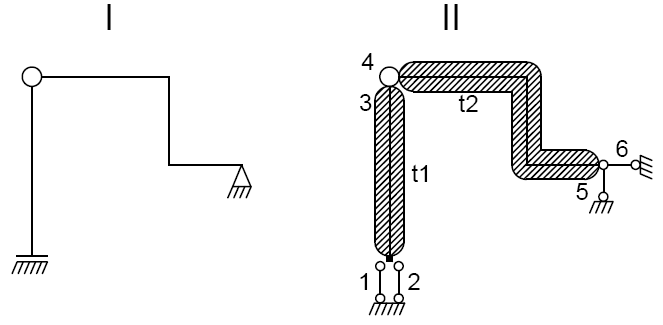
Z powyższego rysunku wynika:
Liczba tarcz:
\[t = 2
\]
Liczba więzi:
\[e = 6
\]
Sprawdzenie warunku:
\[e = 3t
\] \[
6 = 3*2
\] \[
6 = 6
\]
Sprawdzenie powyższego warunku oznacza, że układ jest statycznie wyznaczalny.

Przykład do pobrania



