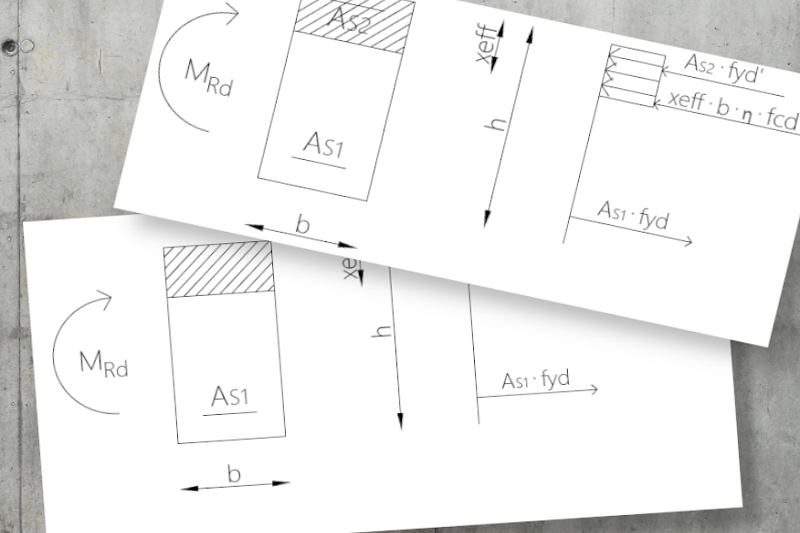
Obliczenie nośności przekroju prostokątnego należy rozpocząć od sprawdzenia czy w analizowanym przekroju uwzględniamy zbrojenie strefy ściskanej, czy też nie. Aby to sprawdzić należy skorzystać z następującej nierówności:
\[S_L ≤ 15 \cdot ϕ
\]
gdzie:
- SL – rozstaw zbrojenia na ścinanie w analizowanym przekroju, wyrażona w [mm],
- ϕ – maksymalna średnica zbrojenia ściskanego (AS2), wyrażona w [mm].
W przypadku, gdy rozstaw zbrojenia poprzecznego na ścinanie w analizowanym przekroju jest mniejszy bądź równy 15-krotności maksymalnej średnicy zbrojenia strefy ściskanej (SL≤15ϕ), to zbrojenie to należy uwzględnić podczas obliczeń nośności. W przeciwnym razie (SL>15ϕ) zbrojenie strefy ściskanej należy pominąć.
Obliczenie nośności przekroju prostokątnego pojedynczo zbrojonego (SL>15ϕ):
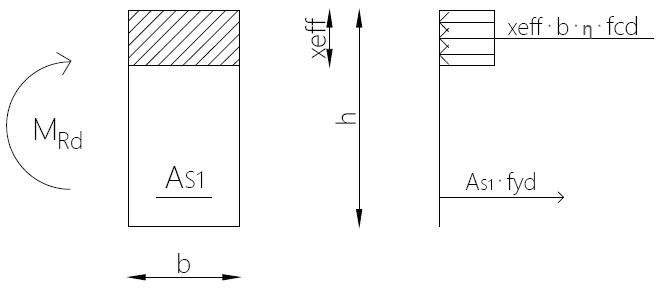
- Wyznaczenie granicznej wartości ξeff,lim :
ξ_{eff,lim} = \frac { λ \cdot ε_{cu2} } {ε_{cu2} + ε_{yd} }
\]
gdzie:
- εcu2 – graniczne odkształcenie betonu,
- εyd – najmniejsze odkształcenie, podczas którego stal osiąga obliczeniową granicę plastyczności (εyd = fyd/Es),
- fyd – wartość obliczeniowa granicy plastyczności stali,
- Es – moduł sprężystości stali,
- λ – stosunek zasięgu strefy naprężeń ściskających do strefy skróceń:
- λ = 0,8, jeżeli: fck ≤ 50 MPa,
- oraz λ = 0,8 – (fck – 50)/400, jeżeli: fck > 50 MPa.
- Wyznaczenie granicznego zasięgu strefy ściskanej:
x_{eff,lim} = ξ_{eff,lim} \cdot d
\]
- Wyznaczenie zasięgu strefy ściskanej:
x_{eff} = \frac {A_{S1} \cdot f_{yd}} {b \cdot η \cdot f_{cd}}
\]
gdzie:
- AS1 – pole zbrojenia,
- fcd – obliczeniowa wytrzymałość betonu na ściskanie,
- d – wysokość użyteczna przekroju: d = h – 0,1⋅h,
- η = 1,0, w przypadku, gdy: fck ≤ 50 MPa,
- η = (fck – 50)/200, w przypadku, gdy: fck > 50 MPa.
- Obliczenie nośności przekroju MRd:
- Gdy xeff ≤ xeff,lim :
M_{Rd} = b \cdot η \cdot f_{cd} \cdot x_{eff} \cdot (d – 0,5 \cdot x_{eff})
\]
- Jeśli xeff > xeff,lim, to do obliczeń nośności przyjmujemy xeff = xeff,lim:
M_{Rd} = b \cdot η \cdot f_{cd} \cdot x_{eff,lim} \cdot (d – 0,5 \cdot x_{eff,lim})
\]
Obliczenie nośności przekroju prostokątnego podwójnie zbrojonego (SL≤15ϕ):
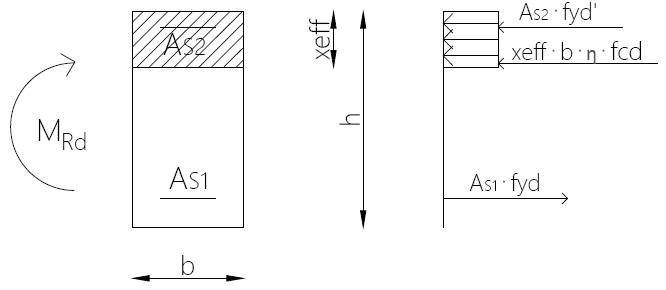
- Wyznaczenie granicznej wartości ξeff,lim :
ξ_{eff,lim} = \frac { λ \cdot ε_{cu2} } {ε_{cu2} + ε_{yd} }
\]
- Wyznaczenie granicznego zasięgu strefy ściskanej:
x_{eff,lim} = ξ_{eff,lim} \cdot d
\]
- Wyznaczenie zasięgu strefy ściskanej:
x_{eff} = \frac {A_{S1} \cdot f_{yd} – A_{S2} \cdot f_{yd}} {b \cdot η \cdot f_{cd}}
\]
- Obliczenie nośności przekroju MRd:
- Jeśli xeff ≤ 2⋅d2, to pomijamy pracę betonu na ściskanie:
M_{Rd} = A_{S1} \cdot f_{yd} \cdot (d – d_2)
\]
gdzie:
- d2 – odległość środka ciężkości zbrojenia górnego licząc od krawędzi ściskanej przekroju.
- Jeśli xeff > 2⋅d2, to przechodzimy do porównania warunku xeff ≤ xeff,lim:
- gdy xeff ≤ xeff,lim to:
M_{Rd} = b \cdot η \cdot f_{cd} \cdot x_{eff} \cdot (d – 0,5 \cdot x_{eff}) + A_{S2} \cdot f_{yd}’ \cdot (d – d_2)
\]
- Jeśli xeff > xeff,lim, to do obliczeń nośności przyjmujemy xeff = xeff,lim:
M_{Rd} = b \cdot η \cdot f_{cd} \cdot x_{eff,lim} \cdot (d – 0,5 \cdot x_{eff,lim}) + A_{S2} \cdot f_{yd} ’ \cdot (d – d_2)
\]
Literatura:
[1] PN-EN 1992-1-1:2008 Eurokod 2 – Projektowanie konstrukcji z betonu – Część 1-1: Reguły ogólne i reguły dla budynków,
[2] PN-B-03264:2002 Konstrukcje betonowe, żelbetowe i sprężone – Obliczenia statyczne i projektowanie.
[3] Knauff, “Obliczanie konstrukcji żelbetowych według Eurokodu 2” Wydawnictwo Naukowe PWN, Warszawa 2012.
Zobacz też:
Odchyłki otulenia prętów zbrojeniowych
Klasy wytrzymałości betonu wg Eurokodu 2 PN-EN 1992