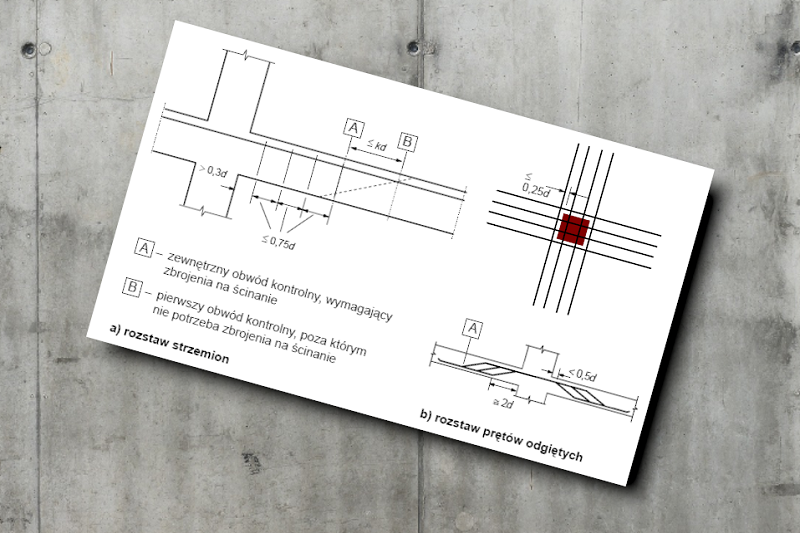
Zbrojenie poprzeczne na ścinanie projektuje się zwykle jako zbrojenie w postaci pionowych strzemion, czasami również strzemion nachylonych pod kątem lub prętów odgiętych otaczających podłużne zbrojenie zlokalizowane w strefie rozciąganej oraz ściskanej. Pręty odgięte czy też ukośne stosuje się w specjalnych przypadkach, gdy maksymalne zbrojenie strzemion jest niewystarczające. Istotne jest, aby strzemiona przenosiły nie mniej niż 50% siły poprzecznej, na którą projektuje się zbrojenie na ścinanie. Oznacza to, że zbrojenie na ścinanie zapewni co najmniej 50% nośności całego zbrojenia. Dlatego też istotny jest rozkład zbrojenia na ścinanie, który powinien odpowiadać temu założonemu w obliczeniach.
Zbrojenie na ścinanie – rozstaw zbrojenia na ścinanie
Minimalny rozstaw zbrojenia na ścinanie nie jest normowany. Należy jednak pamiętać o technologii wykonania elementu (możliwość zagęszczenia mieszanki betonowej). Maksymalny rozstaw zbrojenia na ścinanie jest ograniczony bez względu na wymagania związane z minimalnym polem przekroju zbrojenia poprzecznego. Maksymalny rozstaw zbrojenia na ścinanie można wyznaczyć zgodnie z poniższym wzorem:
\[s_{l,max} = 0,75⋅d⋅(1+ctgα) ≤ 600
\]
gdzie:
d – wysokość użyteczna przekroju,
α – kąt między zbrojeniem na ścinanie i osią podłużną elementu (kąt nachylenia zbrojenia na ścinanie powinien wynosić pomiędzy 45° a 90°),
W przypadku prętów odgiętych ich maksymalny rozstaw podłużny powinien wynosić:
\[s_{l,max} = 0,6 ⋅ d ⋅ (1 + ctgα)
\]
Podłużny rozstaw zbrojenia poprzecznego powinien spełniać następujący warunek:
\[s ≤ 12,5 ⋅ \frac {A_{sw} ⋅ f_{yd} }{b_w ⋅ sinα ⋅ \sqrt {f_{ck} }}
\]
gdzie:
Asw – pole przekroju zbrojenia na ścinanie,
fyd – obliczeniowa granica plastyczności zbrojenia,
bw – szerokość środnika elementu,
fck – charakterystyczna wytrzymałość walcowa na ściskanie betonu po 28 dniach.
Literatura:
[1] PN-EN 1992-1-1:2008 Eurokod 2 – Projektowanie konstrukcji z betonu – Część 1-1: Reguły ogólne i reguły dla budynków,
[2] PN-B-03264:2002 Konstrukcje betonowe, żelbetowe i sprężone – Obliczenia statyczne i projektowanie.
[3] Knauff, “Obliczanie konstrukcji żelbetowych według Eurokodu 2” Wydawnictwo Naukowe PWN, Warszawa 2012.
Zobacz też:
Długość zakładu prętów zbrojeniowych
Długość zakotwienia prętów zbrojeniowych