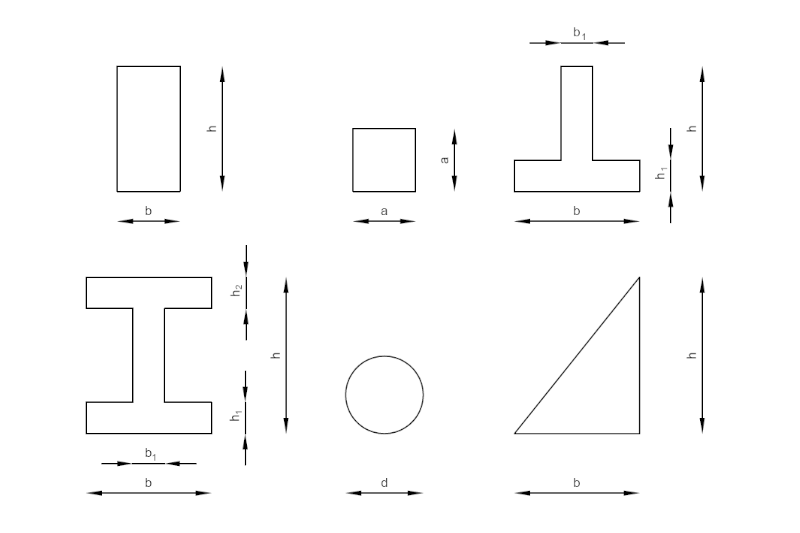
Wykonywane w budownictwie konstrukcje prętowe składają się z figur o różnych kształtach. Konstrukcje wykonane z drewna, żelbetu, stali czy też z elementów murowych mogą mieć różne przekroje, np. kwadratu, prostokąta, dwuteownika, itp. Przekroje poprzeczne prętów wpływają nie tylko na wytrzymałość konstrukcji, ale na jej sztywność. Charakterystyki geometryczne figur płaskich to:
- pole przekroju – A [cm2, m2],
- moment statyczny pola – S [cm3, m3],
- momenty bezwładności – I [cm4, m4],
- wskaźniki wytrzymałości – W [cm3, m3],
- promienie bezwładności – i [cm, m].
Moment statyczny
Moment statyczny pola S obliczany jest w celu wyznaczenia położenia osi środkowych. Położenie środka O w przypadku płaskiej figury geometrycznej można wyznaczyć dla dowolnie przyjętego układu współrzędnych. Osie układów współrzędnych, których początek znajduje się w środku pola figury płaskiej, określany jest jako osie środkowe.
Czym są figury proste? Są to wszystkie figury o znanym środku pola, czyli taki jak: kwadrat, prostokąt, trójkąt, koło. W przypadku założonego układu współrzędnych o osiach a i b, środek dla figury płaskiej ma współrzędne w tym układzie ao oraz bo. Współrzędne można wyznaczyć z poniżej przedstawionych wzorów:
\[a_o= \frac{S_b}{A}
\quad\quad
b_o= \frac{S_a}{A}
\]
gdzie:
Sa, Sb – momenty statyczne pola figur względem osi,
A – pole figury.
W przypadku, gdy oś, względem której obliczany jest moment statyczny, przechodzi przez środek pola. Jego wartość równa się zero. Jeśli przekrój składa się z kilku figur, w takich przypadkach moment statyczny pola obliczany jest jako suma momentów bezwładności dla poszczególnych figur.
Momenty bezwładności
Moment bezwładności pola oznacza się literą I z indeksem osi współrzędnych, według której obliczany był moment bezwładności. Jednostką momentu bezwładności pola jest [cm4, m4]. Moment bezwładności zależy nie tylko od wielkości, ale również od kształtu przekroju poprzecznego. Im większy jest moment bezwładności elementu konstrukcyjnego, tym większa jest jego nośność oraz sztywność.
Wskaźnik wytrzymałości
Wskaźnik wytrzymałości przekroju jest ilorazem momentu bezwładności tego przekroju względem osi obojętnej (przechodzącej przez środek ciężkości przekroju) przez odległość od osi najdalej położonego elementu w danym przekroju.
Promień bezwładności
Promień bezwładności wyrażany jest w jednostce [cm, m]. Jest to pierwiastek ilorazu momentu bezwładności oraz pola przekroju danej figury.
Wielkości charakteryzujące przekroje oblicza się względem osi głównych [y, z], przechodzących przez środki ciężkości przekrojów. Poniżej przedstawiono momenty bezwładności wraz ze wskaźnikami wytrzymałości dla wybranych figur płaskich:
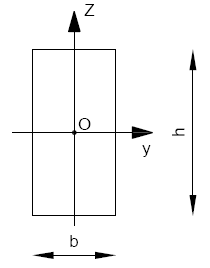
Momenty bezwładności:
\[I_y= \frac{b \cdot h^3}{12}
\quad\quad
I_z= \frac{h \cdot b^3}{12}
\]
Wskaźniki wytrzymałości:
\[W_y= \frac{b \cdot h^2}{6}
\quad\quad
W_z= \frac{h \cdot b^2}{6}
\]
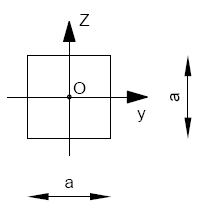
Momenty bezwładności:
\[I_y= I_z= \frac{a^4}{12}
\]
Wskaźniki wytrzymałości:
\[W_y= W_z= \frac{a^3}{6}
\]
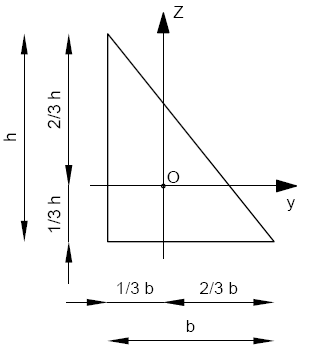
Momenty bezwładności:
\[I_y= \frac{b \cdot h^3}{36}
\quad\quad
I_z= \frac{h \cdot b^3}{36}
\]
Wskaźniki wytrzymałości:
\[W_y= \frac{b \cdot h^2}{12}
\quad\quad
dla
\quad\quad
e =|\frac{1}{3} \cdot h|
\] \[
W_y= \frac{b \cdot h^2}{24}
\quad\quad
dla
\quad\quad
e =|\frac{2}{3} \cdot h|
\] \[
W_z= \frac{h \cdot b^2}{12}
\quad\quad
dla
\quad\quad
e =|\frac{1}{3} \cdot b|
\] \[
W_z= \frac{h \cdot b^2}{24}
\quad\quad
dla
\quad\quad
e =|\frac{2}{3} \cdot b|
\]
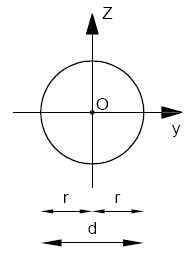
Momenty bezwładności:
\[I= \frac{π \cdot r^4}{4} = \frac{π \cdot d^4}{64}
\quad\quad
\]
Wskaźniki wytrzymałości:
\[W= \frac{π \cdot r^3}{4} = \frac{π \cdot d^3}{32}
\quad\quad
\]