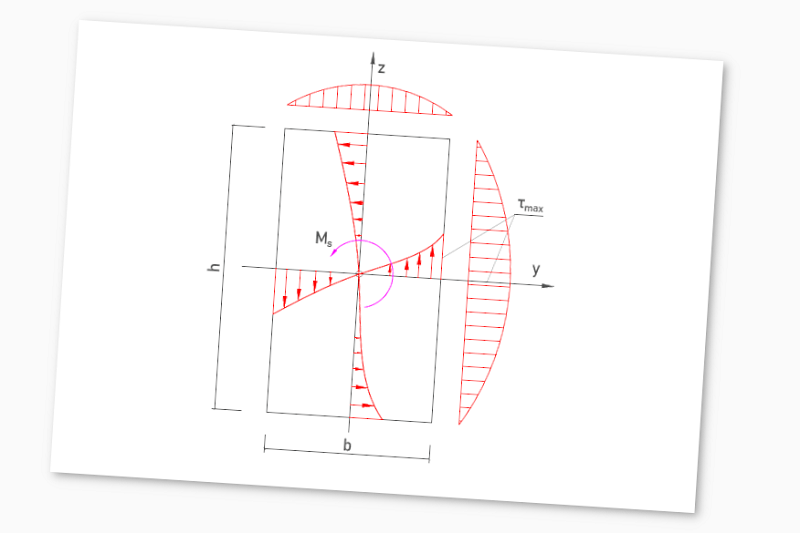
Elementy żelbetowe można klasyfikować w zależności od sposobu ich obciążenia. Jednym z nich są elementy obciążone momentem skręcającym. Skręcanie elementów żelbetowych następuje w przypadku, gdy wypadkowa sił działa na mimośrodzie w stosunku do osi podłużnej elementu. W praktyce do elementów skręcanych żelbetowych można zaliczyć np.: skrajne belki stropów, belki/wieńce mocujące płyty balkonowe, ramy przestrzenne, itp. Poniżej przedstawiono rysunek prezentujący rozkład naprężeń w przypadku skręcanych elementów żelbetowych:
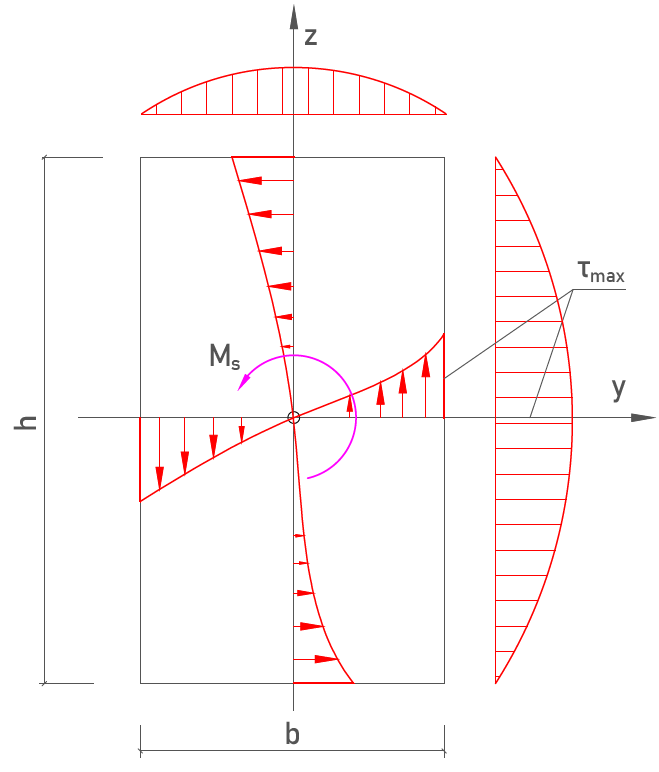
Na podstawie powyższego rysunku można zaobserwować, że największe naprężenia styczne występują dokładnie w połowie rozpiętości dłuższego boku danego przekroju. Najmniejsze naprężenie można natomiast zaobserwować w narożach, ale również w środku przekroju.
Skręcanie elementów żelbetowych według Eurokodu 2
Według Eurokodu 2 nośność elementów skręcanych należy obliczać, jak w przypadku cienkościennego przekroju zamkniętego. Oznacza to, że przekroje pełnościenne zostają zastąpione przez równoważne przekroje cienkościenne. Z przekrojów innych niż prostokątne (np. przekroje teowe) należy wydzielić odrębne części, które rozpatruje się jako przekroje cienkościenne, nośność przekroju w takim przypadku to suma nośności wydzielonych części. Efektywną grubość ścianek tef,i w przekroju cienkościennym należy wyznaczyć według wzoru:
\[t_{ef,i} = \frac{A_i}{u_i}
\]
gdzie:
Ai – pole przekroju ograniczonego przez zewnętrzny obwód liczony wraz z otworami,
ui – długość zewnętrznego obwodu przekroju.
Naprężenie styczne w ścianie przekroju można wyznaczyć według następującego wzoru:
\[τ_{t,i} = \frac{T_{Ed}}{2A_k \cdot t_{ef,i} }
\]
gdzie:
TEd – obliczeniowy moment skręcający,
Ak – pole powierzchni wnętrza figury powstałej przez linie środkowe ścian (łącznie z polem przekroju pustej części wewnętrznej).
Skręcanie ze ścinaniem
Skręcanie ze ścinaniem to przypadek, w którym naprężenia styczne powstają w wyniku momentu skręcającego oraz sił poprzecznych działających na element. W przypadku, gdy naprężenia powstałe przez ścinanie i skręcanie są nieduże, to obliczenie zbrojenia poprzecznego nie jest koniczne. W innym wypadku należy obliczyć zbrojenie poprzeczne i podłużne. Ze względu na nośność betonu (krzyżulców ściskanych) należy spełnić poniższy warunek:
\[\frac{T_{Ed}}{T_{Rd,max}}+\frac{V_{Ed}}{V_{Rd,max}} ≤1,0
\]
gdzie:
TEd – obliczeniowy moment skręcający,
VEd – obliczeniowa siła poprzeczna,
TRd,max – obliczeniowa nośność na skręcanie:
T_{Rd,max}=2ν \cdot α_{cw} \cdot f_{cd} \cdot A_k \cdot t_{ef,i}\cdot sinθ \cdot cosθ
\] \[
ν =0,6⋅(1− \frac{f_{ck}}{250})
\]
αcw=1,0 – w przypadku konstrukcji niesprężonych,
fck – charakterystyczna wytrzymałość walcowa na ściskanie betonu po 28 dniach,
fcd – obliczeniowa wytrzymałość betonu na ściskanie,
VRd,max – maksymalna nośność obliczeniowa na ścinanie:
\[V_{Rd,max} = α_{cw}\cdot ν \cdot f_{cd} \cdot b_w \cdot z \cdot \frac {ctgθ}{1+ctg^2 θ}
\]
W przypadku, gdy zbrojenie poprzeczne jest zbędne, należy spełnić następujący warunek:
\[\frac{T_{Ed}}{T_{Rd,c}}+\frac{V_{Ed}}{V_{Rd,c}} ≤1,0
\]
gdzie:
θ – kąt nachylenia krzyżulców ściskanych,
TRd,c – to moment skręcający, który oblicza się przyjmując τt,i=fctd:
T_{Rd,c} = 2 \cdot A_K \cdot t_{ef,i} \cdot f_{ctd}
\]
VRd,c – wartość obliczeniowa nośności na ścinanie:
\[V_{Rd,c} = ν_{Rd,c} \cdot b_w \cdot d
\]
gdzie:
\[ν_{Rd,c}= \frac{0,18}{γ_c} \cdot k \cdot (100 \cdot ρ_l⋅f_{ck})^{1/3}+ 0,15 \cdot σ_{cp}
\]
lecz nie mniej niż:
\[ν_{Rd,c}= v_{min}+ 0,15 \cdot σ_{cp}
\]
Obliczenie zbrojenia poprzecznego i podłużnego
Zbrojenie poprzeczne należy wyznaczyć, jak w przypadku wymiarowania jednego strzemienia:
\[A_{sw} = \frac {0,5⋅T_{Ed}}{A_k⋅f_{ywd}⋅cotθ}
\]
gdzie:
Asw – pole przekroju ramienia strzemienia,
fywd – obliczeniowa granica plastyczności stali strzemion,
sw – rozstaw podłużny ramion obliczany według wzoru:
S_w = τ_{t,i} \cdot t_{ef,i} = \frac{T_{Ed}}{2A_k}
\]
Zbrojenie podłużne wyznacza się według następującego wzoru:
\[A_{sl} = \frac {T_{Ed}⋅u_k⋅cotθ}{2⋅A_k⋅f_{yd}}
\]
gdzie:
uk – to obwód pola Ak,
fyd – jest obliczeniową granicą plastyczności zbrojenia podłużnego.
Bibliografia:
[1] PN-EN 1992-1+AC+Ap 1,2,3: 2008, Projektowanie konstrukcji z betonu, Część 1-1: Reguły ogólne i reguły dla budynków.
Zobacz też:
Zbrojenie poprzeczne na ścinanie