Do typowych elementów ściskanych zalicza się słupy, a także ściany oraz tarcze. W praktyce podłużne siły ściskające zawsze działają na element na pewnym mimośrodzie. Są to tak zwane mimośrody przypadkowe powstałe w wyniku odchyleń od przyjętych założeń projektowych. W związku z tym sposób ściskania elementów nie jest jednoznaczny. W przypadku ściskania osiowego mimośród ee=0, w pozostałych przypadkach mimośród jest różny od zera. Elementy ściskane mimośrodowo to takie, w których w przekroju poprzecznym występuje obliczeniowy moment zginający Msd oraz siła podłużna ściskająca Nsd, które w obliczeniach zastępuje się przez siłę Nsd działającą na mimośrodzie konstrukcyjnym ee=Msd/Nsd odmierzanym od osi ciężkości elementu uwzględniając wyłącznie część betonową (bez uwzględnienia zbrojenia). Jeśli w obliczeniach nośności uwzględnia się dodatkowo wpływ smukłości elementu, to mimośród ee określa się następująco:
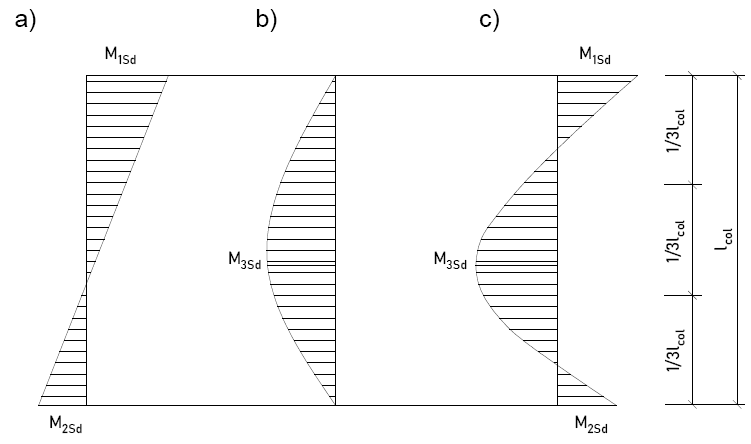
a) w przypadku elementów w układzie ramowym z węzłami nieprzesuwnymi – rozkład momentów zginających prostoliniowy wzdłuż elementu:
\[e_{e} =| \frac {0,6M_{1Sd} + 0,4M_{2Sd}}{N_{sSd}}|
\]
lecz nie mniej niż:
\[e_{e} =| \frac {0,4M_{1Sd}}{N_{sSd}}|
\]
b) w przypadku elementów o krzywoliniowym rozkładzie momentów zginających wzdłuż elementu:
\[e_{e} =| \frac {M_{3Sd}}{N_{sSd}}|
\]
gdzie:
M1Sd, M2Sd – to wartości momentów zginających na końcach elementu przy czym: |M1Sd|≥|M2Sd|,
M3Sd – ekstremalna wartość momentu zginającego, występująca na środkowym odcinku równym 1/3 długości elementu.
c) jeśli element występuje w układzie ramowym o węzłach przesuwnych:
\[e_{e} =| \frac {M_{Sd}}{N_{sSd}}|
\]
gdzie:
MSd – to ekstremalna wartość momentu zginającego występująca na całej długości elementu.
Mimośród początkowy i wpływ smukłości
Mimośród początkowy siły ściskającej w stosunku do środka ciężkości przekroju betonu można wyznaczyć według wzoru:
\[e_{0} = e_{a} + e_{e}
\]
gdzie:
ea – to niezamierzony mimośród przypadkowy, spowodowany np. krzywizną elementu, odchyłkami od założonego usytuowania elementu konstrukcji, różnymi cechami wytrzymałościowymi materiału itp.,
ee – mimośród konstrukcyjny, równy ilorazowi momentu zginającego MSd oraz siły podłużnej NSd spowodowanych obciążeniem obliczeniowym.
Wartość niezamierzonego mimośrodu przypadkowego ea należy przyjąć jako największa z niżej podanych wartości:
- W ustrojach ścianowych i w ustrojach szkieletowych o węzłach nieprzesuwnych, gdzie lcol – odległość między punktami podparcia elementu, a w przypadku elementu wspornikowego – jego długością:
e_a = \frac{l_{col}}{600}
\]
- W ustrojach szkieletowych o węzłach przesuwnych dla elementów n-tej kondygnacji licząc od góry:
e_a = \frac{l_{col}}{600}\cdot(1+\frac{1}{n})
\]
lub:
\[e_a = \frac{h}{30}
\]
gdzie:
h – wysokość przekroju betonu w rozpatrywanej płaszczyźnie,
- w przypadku konstrukcji monolitycznych oraz prefabrykowanych ścian i powłok:
e_a = 10 mm
\]
- w przypadku konstrukcji prefabrykowanych z wyjątkiem ścian i powłok:
e_a = 20 mm
\]
Nośność elementów ściskanych
Nośność elementów ściskanych należy sprawdzić uwzględniając smukłość elementów dla których:
- w przypadku elementów betonowych:
\frac{l_0}{i}>20
\]
oraz dla przekroju prostokątnego:
\[\frac{l_0}{h}>6
\]
- w przypadku elementów żelbetowych i sprężonych:
\frac{l_0}{i}>25
\]
oraz dla przekroju prostokątnego:
\[\frac{l_0}{h}>7
\]
gdzie:
l0 – długość obliczeniowa wraz z uwzględnieniem sposobu podparcia.
Wpływ smukłości na nośność ściskanych elementów żelbetowych
Wpływ smukłości należy uwzględnić w obliczeniach poprzez zwiększenie mimośrodu początkowego e0 na mimośród etot wyznaczanego według wzoru:
\[e_{tot} = η\cdot e_0
\]
w którym:
\[η = \frac {1}{ 1 – \frac{N_{Sd}}{N_{crit}}}
\]
Wartość Ncrit należy wyznaczyć według wzoru:
\[N_{crit} = \frac {9}{l_0^2}\cdot [ \frac {E_{cm}\cdot{I_c}}{2\cdot k_{lt}}\cdot( \frac {0,11}{0,1+ e_0/h}+0,1)+E_s \cdot I_s]
\]
gdzie:
Ic – moment bezwładności przekroju betonu względem jego środka ciężkości,
Is – moment bezwładności przekroju zbrojenia względem środka ciężkości przekroju betonu.
Wartość stosunku e0/h zależna od mimośrodu obciążenia, lecz nie mniej niż:
\[e_0/h = 0,50-0,01 \cdot l_0/h – 0,01 \cdot f_{cd}≥0,05
\]
gdzie:
fcd – wytrzymałość obliczeniowa betonu na ściskanie w elementach niezbrojonych wyrażona w MPa.
Współczynnik klt uwzględniający wpływ oddziaływania długotrwałego należy wyznaczyć według wzoru:
\[k_{lt} = 1 + 0,5 \cdot \frac {N_{Sd,lt}}{N_{Sd}} \cdot ∅(α,t_0)
\]
gdzie:
NSd,lt – siła podłużna ściskająca spowodowana działaniem długotrwałej części obciążenia obliczeniowego,
∅(α,t0) – końcowy współczynnik pełzania betonu.
Zobacz też:
Zbrojenie poprzeczne na ścinanie